Fourier Transform Nano-Dynamical Mechanical Analyzer
(nanoindenting AFM extension)
(nanoindenting AFM extension)
A nanoindenter AFM extension allows for measurement of (quasi)static and dynamic mechanical moduli of soft materials (roughly defined as the ones with Young’s modulus <50GPa). This patented technique allows for highly quantitative measurements of static (Young’s) and dynamic (storage and loss) moduli up to 300-500Hz which are the most relevant for soft- and bio- materials. Such limit can be extended to 2-3KHz upon request.
FT-nanoDMA™ represents a novel method of studying dynamic mechanical spectra (DMS) of soft materials with resolutions substantially superior to existing state of the art nanoindenters. This allows the extension of DMS measurements to scales previously inaccessible (for example, the study of individual biological cells). This method can be used in virtually any environment suitable for AFM operation.
The idea of FT-nanoDMA™ method is the use of multiple frequencies simultaneously. This alone decreases the measurement time proportionally to the number of frequencies, even as it allows the receipt of measurements faster than the time needed waiting for creep relaxation. As a result, measurement time is decreased approximately 100x when measuring 10 frequencies simultaneously. Furthermore, by avoiding creep relaxation, the lateral resolution is improved by the same factor of approximately 100x. See the values in the table below, in which the contact diameter (de facto lateral resolution) is compared to the best obtained with the current state of the art nanoindenters. Note that the contact diameter may look a bit large compared to the typical contact size of AFM probe and sample. However, this is the minimum contact size needed to work in the linear stress-strain regime; i.e. to obtain information from elastic moduli correctly.
FT-nanoDMA’s highly accurate technique is based upon a combination of three different methods:
Comparison of FT-nanoDMA™ method with existing nanoindentation method - quantitative nanoindentation (nanoDMA);
- gentle force and fast response of atomic force microscopy (AFM); and
- Fourier transform (FT) spectroscopy.
- Provides a substantially higher spatial resolution (50-150x for lateral and 30-150x for vertical). Such an improvement is comparable to the technological leap of optical to electron microscopy for soft materials.
- Increases the speed (70-180x) of mapping viscoelastic properties of soft materials. In practical terms, this means a reduction in measurement time from hours/ weeks to minutes/hours.
- Enables measurements of mechanical properties of many biological materials, for which measurement time is typically limited.
- Allows for testing of the linearity of strain-stress relation at the nanoscale.
- Provides highly quantitative results.
| Property | TI 950 Hysitron nanoindenter- based nanoDMA | AFM-based FT-nanoDMA |
| Contact diameter | 22,000 or 33,000 nm (PDMS) | 160 or 230 nm (PDMS) |
| 9,000 or 15,000 nm (polyurethane) | 140 or 170 nm (polyurethane) | |
| Minimum vertical indentation | 1000 or 2600 nm (PDMS) | 100 or 400 nm (PDMS) |
| 100 or 300 nm (polyurethane) | 5 or 10 nm (polyurethane) | |
| Total measurement time at one point of the surface | >200 sec (for 10 frequencies) | ~0.7–1 sec (for 10 frequencies though the number of frequencies is not a limiting factor) |
| Time to record 100 × 100 pixel map | 23 days (impractical) | 1.9 hours |
| Ability to study individual biological cells | no | yes |
| Frequency range | Up to 300 Hz | Up to 300 Hz |
The above comparison is done using the same samples of two polymers: PDMS resin (the Young’s modulus of 1.5 MPa) and polyurethane (the Young’s modulus of 0.63 GPa).
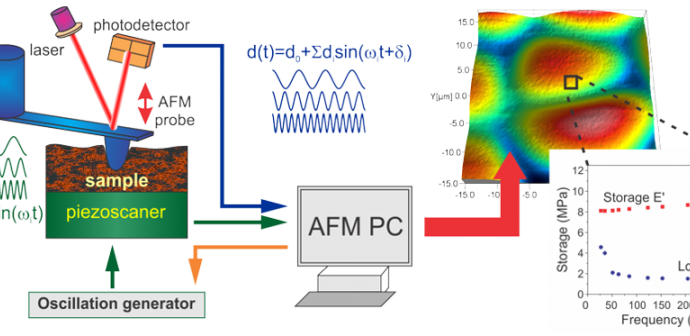
Scheme of FT-nanoDMA setup
An AFM probe indents the sample with a predefined force at each point of the mapped surface. Oscillations of multiple frequencies are simultaneously sent to a piezoscanner that oscillates the sample with total amplitude of z(t). The oscillations are detected through the deflection of the AFM probe d(t). By using the Fourier transformation of the total deflection signal, amplitudes and phase shifts for each frequency can be found. The values of the recorded amplitudes and phases are used to calculate the storage and loss moduli as well as other parameters characterizing the sample.
